| PAGE 1 OF 3 | [1] [2] [ref] | DOWNLOAD PDF |
Reprinted from Proc. Royal Society B 171 179-296 with the kind permission of the Editor
[This paper develops the notion of perceptual hypotheses and also raises questions concerning the distinction to be made between 'analogue' and 'digital'. This is made in the context of the brain, and seems important if we are to be clear in how we use an engineering distinction. The point is: Should the distinction be regarded as one of engineering convenience (continuous or discontinuous mechanisms, or circuits) or should it be regarded as a deeper logical distinction? I incline to the latter view.]
An adequate theory of visual perception must explain how the fleeting patterns of light upon the retinas give knowledge of surrounding objects. The problem of how the brain 'reads' reality from images is acute, because images represent directly but few, and biologically unimportant, characteristics of objects. What matters biologically are such things as whether an object is poisonous or food, hard or soft, heavy or light, sharp or blunt, friend or foe. These are not properties of images. The owner of the eye cannot eat or be eaten by its images, and yet his life depends upon interpreting them in terms of quite different characteristics of objects. It follows that eyes are of little biological value unless there is an adequate brain to interpret their images; which raises the evolutionary problem: how did the eye-brain combination arise? (cf. Gregory, 1968c [REF 9]). To read reality from images is to solve a problem: a running set of very difficult problems throughout active life. Errors are illusions. Certain situations present special difficulty, giving rise to systematic errors: can these serve as clues to how the brain generally solves the problem of what objects are represented by which images?
Illusions can occur in any of the sense modalities, and they can cross the senses. A powerful illusion crosses from the seen size of an object to its apparent weight, as judged by lifting. Small objects feel up to fifty per cent heavier than larger objects of the same scale weight. Thus weight is evidently not judged simply by the input from the arm but also by prior expectation set by the previous handling of weights. When the density is unexpectedly great or small we suffer a corresponding illusion of weight.
 Click to rotate. Click to stop.
Click to rotate. Click to stop.
FIG. 1 Spiral. When rotating anticlockwise it is seen to contract. If stopped after ten to twenty seconds viewing, a marked apparent expansion is observed. There is however no observed change in size. It seems that a specific velocity-detecting system has been adapted by the real movement.
There are, however, illusions of quite different types. There are purely optical illusions, where light from the object to the eye is bent by reflection (mirrors) or by refraction (the bent-stick-in-water effect, and mirages). There are also what we may call sensory illusions. The sense organs, the eyes, ears, touch and heat-sensitive nerve endings can all be upset, when they will transmit misleading information to the brain. They are upset by prolonged stimulation and by over-stimulation. For example, the 'waterfall effect' observed by Aristotle, is dramatically demonstrated by watching a rotating spiral (Fig. 1). If this is rotated on a turntable for ten or twenty seconds while the eyes are held at its centre, it will seem to contract or expand, depending on the direction of rotation. When stopped, there is a marked illusory movement in the opposite direction to the original movement. In the illusion, movement is seen but with no change of position.
Evidently a velocity detecting system has been adapted by prolonged stimulation to movement. As is well known, after-images occur after intense or prolonged stimulation of the retina by light: we see first a positive 'picture' which soon changes to a negative 'picture' which may persist for many minutes. This is due to local retinal adaptation, the brain receiving retinal signals essentially the same as for the normal image of an object but persisting beyond the physical stimulation of the retina. It is also possible for any sense organ to signal a quite wrong kind of stimulus. Pressure on the eye will send signals to the brain which are experienced as light; and electric current through the eye will produce the sensation of light, and through the ear sound. Fortunately, these sensory illusions seldom occur in normal conditions, though they are easily evoked in the laboratory.
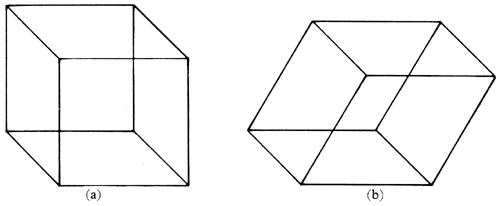
FIG. 2 (a) Necker cube. This is the most famous of many depth-ambiguous, figures. (When presented with no background it changes in shape with each reversal, the apparent back being larger than the apparent front face.) (b) Necker rhomboid. This is the original form, presented by L. A. Necker in 1832.
The types of illusions which concern us here are, however, entirely different from either optical or sensory illusions. We may call these perceptual illusions. They arise from misinterpretation by the brain of sensory information.
Several perceptual illusions were known to the ancient Greeks, but they have only been studied experimentally for just over a century. The first scientific description in modern times was a letter by a Swiss naturalist, L. A. Necker, to Sir David Brewster (Necker, 1832) describing how a rhomboid reverses in depth, sometimes one face appearing the nearer, sometimes another. Necker correctly noted that changes of eye fixation could induce this change in perception, but that it would occur quite spontaneously. This famous effect is generally illustrated with an isometric skeleton cube (Fig. 2 a) rather than Necker's original figure (Fig. 2b). Perceptual reversals, or alternations (there can be several alternative perceptions) are not limited to vision. Repeated words, presented on an endless tape loop, give analogous auditory reversals (Warren and Gregory 1958 [REF 3]); A similar, even more striking effect, was noted by W. J. Sinsteden: that the rotating vanes of a windmill spontaneously reverse direction when it is not clear whether one is seeing the front or the back of the windmill (for references, see Boring, 1942). This effect is well shown by casting the shadow of a slowly rotating vane upon a screen, thus removing all information of which is the back and which the front. The shadow will also at times appear to expand and contract upon the plane of the screen. It is important to note that these effects are not perceptual distortions of the retinal image: they are alternative interpretations of the image, in terms of possible objects, and only one interpretation is correct.
The most puzzling visual illusions are systematic distortions of size or shape. These distortions occur in many quite simple figures; the distortions occurring in the same directions and to much the same extent in virtually all human observers and probably also in many animals. Their explanation presents a challenge which should be accepted, for a viable theory of normal perception must account for them and they could be important clues to basic perceptual processes.
The simplest distortion illusion was the first to be described: by the father of experimental psychology, Wilhelm Wundt (1832 - 1920), who was Hermann von Helmholtz's assistant at Heidelburg. Wundt described the 'horizontal - vertical' illusion - that a vertical line looks longer than the horizontal line of equal length. He attributed this distortion to asymmetry of the eye movement system. Although this has been invoked many times since to explain distortion illusions it must be ruled out, for the distortions occur in after-images, or in normal retinal images optically stabilized so as to remain stationary on the eye though it moves. In addition, distortions can occur in several directions at the same time, which could hardly be due to eye movements; and in any case it is difficult to see how curvature distortions could be related to eye movements. All the evidence points to the origin of the distortions being not in the eyes but in the brain.
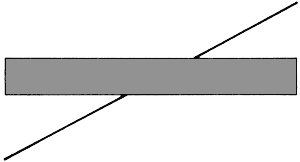
FIG. 3 The Poggendorff illusion figure (1860). The straight line crossing the rectangle appears displaced.
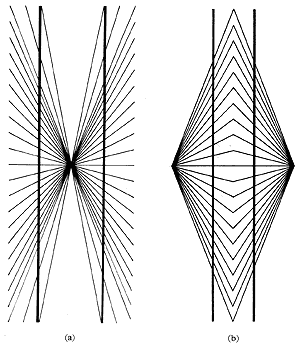
FIG. 4 (a) Hering illusion (1861) The straight parallel lines appear bowed outwards. (b) Wundt's variant of the Hering illusion: the parallel lines appear bowed inwards (1896).
Interest in the illusions became general upon the publication of several figures showing distortions which could produce errors in using optical instruments. This concerned physicists and astronomers a hundred years ago, when photographic and other ways of avoiding visual errors were not available. The first of the special distortion figures was the Poggendorff figure of 1860 (Fig. 3). This was followed by the Hering illusion (1861); its converse being devised by Wundt much later, in 1896 (Thiéry 1896) (FIG. 4). The most famous illusion of all is the Müller-Lyer arrow figure (FIG. 5). This was devised by F. C. Müller-Lyer and was first presented in fifteen variants (Müller-Lyer, 1889). This figure is so simple, and the distortion so compelling that it was immediately accepted as the primary target for theory and experiment. All sorts of theories were advanced: Wundt's eye movement theory (in spite of its inadequacy); that the 'wings' of the arrow heads drew attention away from the ends of the central line, or 'arrow shaft', to make it expand or contract; that the heads induced a state of empathy in the observer (though the distortion seems far too constant for such an explanation), that the distortion is a special case of a supposed general principle that acute angles tend to be overestimated and obtuse angles underestimated.
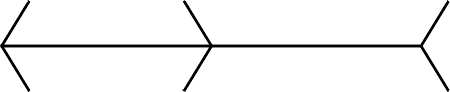
FIG. 5 Müller-Lyer arrows figure 1889. The most famous illusion: the outward-going 'arrow heads' produce expansion of the 'shaft' and the inward-going heads contraction.
This was, however, left unexplained, and it is not clear why it should produce size changes without apparent changes of angle. All these theories had a common feature: they were attempts to explain the distortion in terms of the stimulus pattern without reference to its significance in terms of the perception of objects. There was, however, one quite different suggestion made by A. Thiéry (1896) that the distortions are related to perspective depth features. Thiéry regarded the Müller-Lyer arrows as drawings of such objects as a saw-horse, seen in three dimensions, with the legs going away from the observer in the acute-angled figure and towards him in the obtuse-angled figure. This suggestion has seldom been considered until recently, though the 'perspective theory' was described by R. H. Woodworth in 1938: 'In the Müller-Lyer figure the obliques readily suggest perspective and if this is followed one of the vertical lines appears farther away and therefore objectively longer than the other'. This quotation brings out the immediate difficulties of developing an adequate theory along these lines, for the distortion occurs even when the perspective suggestion is not followed up, for the figure generally appears flat and yet distorted; and there is no hint given of a modus operandi, or brain mechanism responsible for the size changes. An adequate theory following Thiéry's suggestion that perspective is somehow important must show how distortion occurs though the figures appear flat. It should also indicate the kind of brain mechanisms responsible.
 |
 |
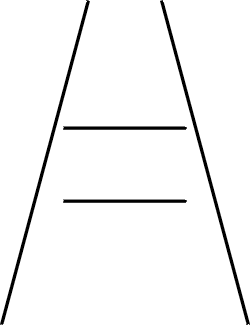
| FIG. 6 Ponzo figure. The upper of the parallel lines is expanded with respect to the lower. | FIG. 7 The Ponzo illusion is seen in this photograph of receding (railway) lines. Here the perspective significance of converging lines is obvious. |
The idea that geometrical perspective - the converging of parallel lines with distance - has a bearing is at least borne out by the occurrence of these distortions in actual scenes. A simple example is the Ponzo illusion (FIG. 6). This is a skeleton drawing of typical perspective convergence of parallel lines with distance, as in the railway lines of Figure 7, (cf. Tausch, 1954). The upper superimposed rectangle, which would be more distant, is expanded. Similarly, the inside corner is expanded (FIG. 8a) and the outside corner shrunk (Fig. 8b) just as in the Müller-Lyer figures, which are like skeleton corners. In both cases, regions indicated by perspective as distant are expanded, while near regions are shrunk. The distortions are opposite to the normal shrinkings of the retinal image of objects with increased distance. Is this merely fortuitous, or is it a clue to the origin of the illusions? Before we come to grips with the problem of trying to develop an adequate perspective theory, it will be helpful to consider some curious features of ordinary pictures.
 |
 |
| FIG 8 (a) The outward-going fins of the Müller-Lyer figure are here seen in flat projection of a photograph of the inside corner of a room. | FIG 8 (b) The inward-going arrows are seen in the outside corner of the building. As in the Ponzo example, distance indicated by perspective is associated with illusory expansion. |
continues